Excerpt from "Self-Organizing Maps in Natural Language Processing".
The basic Self-Organizing Map (SOM) can be visualized as a sheet-like neural-network array (see Figure 1), the cells (or nodes) of which become specifically tuned to various input signal patterns or classes of patterns in an orderly fashion. The learning process is competitive and unsupervised, meaning that no teacher is needed to define the correct output (or actually the cell into which the input is mapped) for an input. In the basic version, only one map node (winner) at a time is activated corresponding to each input. The locations of the responses in the array tend to become ordered in the learning process as if some meaningful nonlinear coordinate system for the different input features were being created over the network (Kohonen, 1995c).
The SOM was developed by Prof. Teuvo Kohonen in the early 1980s (Kohonen, 1981a, 1981b, 1981c, 1981d, 1982a, 1982b). The first application area of the SOM was speech recognition, or perhaps more accurately, speech-to-text transformation (Kohonen et al., 1984,Kohonen, 1988).
Assume that some sample data sets
(such as in Table 1)
have to be mapped onto the array
depicted in Figure 1;
the set of input samples is described by a real vector ![]() where t is the index of the sample,
or the discrete-time coordinate.
Each node i in the map contains a model
vector
where t is the index of the sample,
or the discrete-time coordinate.
Each node i in the map contains a model
vector ![]() ,which has the same number of elements
as the input vector
,which has the same number of elements
as the input vector ![]() .
.
The stochastic SOM algorithm performs a regression process.
Thereby, the initial values of the components of the model
vector, ![]() , may even be selected at random.
In practical applications, however,
the model vectors are more profitably
initialized in some orderly fashion, e.g., along
a two-dimensional subspace spanned by the
two principal eigenvectors of the input data vectors (Kohonen, 1995c).
Moreover, a batch version of the SOM algorithm may also
be used (Kohonen, 1995c).
, may even be selected at random.
In practical applications, however,
the model vectors are more profitably
initialized in some orderly fashion, e.g., along
a two-dimensional subspace spanned by the
two principal eigenvectors of the input data vectors (Kohonen, 1995c).
Moreover, a batch version of the SOM algorithm may also
be used (Kohonen, 1995c).
| 250 | 235 | 215 | antique white |
| 165 | 042 | 042 | brown |
| 222 | 184 | 135 | burlywood |
| 210 | 105 | 30 | chocolate |
| 255 | 127 | 80 | coral |
| 184 | 134 | 11 | dark goldenrod |
| 189 | 183 | 107 | dark khaki |
| 255 | 140 | dark orange | |
| 233 | 150 | 122 | dark salmon |
| ... | ... | ... | ... |
Any input item is thought to be mapped into
the location, the ![]() of
which matches best with
of
which matches best with ![]() in some metric.
The self-organizing algorithm creates the ordered
mapping as a repetition of
the following basic tasks:
in some metric.
The self-organizing algorithm creates the ordered
mapping as a repetition of
the following basic tasks:
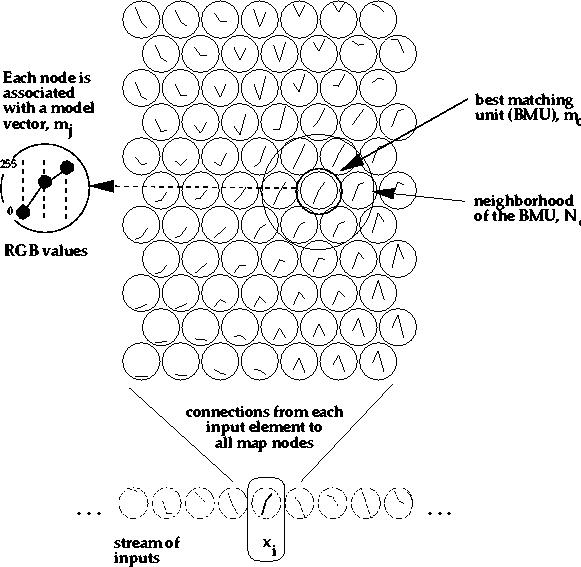 |
The basic idea in the SOM learning process
is that, for each sample input vector ![]() ,the winner and the nodes in its
neighborhood are changed closer to
,the winner and the nodes in its
neighborhood are changed closer to ![]() in the
input data space.
During the learning process, individual changes
may be contradictory,
but the net outcome in the process
is that ordered values for the
in the
input data space.
During the learning process, individual changes
may be contradictory,
but the net outcome in the process
is that ordered values for the ![]() emerge over the array.
If the number of available input samples
is restricted, the samples must be presented
reiteratively to the SOM algorithm.
The random initial state, two intermediate states,
and the final map
are shown in Figure 2.
emerge over the array.
If the number of available input samples
is restricted, the samples must be presented
reiteratively to the SOM algorithm.
The random initial state, two intermediate states,
and the final map
are shown in Figure 2.
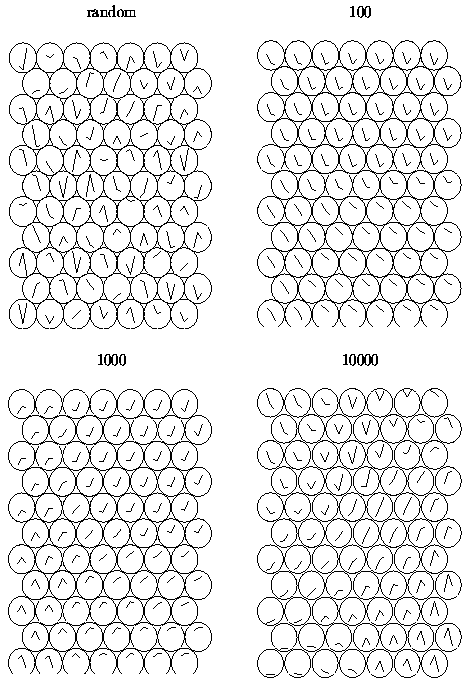 |
Adaptation of the model vectors in the learning process may take place according to the following equations:
(1)
otherwise,
where t is the discrete-time index of the variables,
the factor ![]() is a scalar that defines
the relative size of the learning step, and
Nc(t) specifies the neighborhood around the winner
in the map array.
is a scalar that defines
the relative size of the learning step, and
Nc(t) specifies the neighborhood around the winner
in the map array.
At the beginning of the learning process the radius of the
neighborhood is fairly large, but it
is made to shrink during learning.
This ensures that the global order is obtained
already at the beginning, whereas towards the end,
as the radius gets smaller, the local corrections of the
model vectors in the map will be more specific.
The factor ![]() also decreases during learning.
also decreases during learning.
 |
One method of evaluating the quality of
the resulting map is to calculate
the average quantization error over the input samples,
defined as E![]() where c indicates the best-matching unit for x.
After training,
for each input sample vector the best-matching unit in the
map is searched for,
and the average of the respective quantization errors is
returned.
where c indicates the best-matching unit for x.
After training,
for each input sample vector the best-matching unit in the
map is searched for,
and the average of the respective quantization errors is
returned.
The mathematical analysis of the algorithm has turned out to be very difficult. The proof of the convergence of the SOM learning process in the one-dimensional case was first given in (Cottrell and Fort, 1987). Convergence properties are more generally studied, e.g., in (Erwin et al., 1991,Erwin et al., 1992a,Erwin et al., 1992b,Horowitz and Alvarez, 1996,Flanagan, 1997). A number of details about the selection of the parameters, variants of the map, and many other aspects have been covered in the monograph (Kohonen, 1995c). The aim of this work is not to study or expound the mathematical and statistical properties of the SOM. The main point of view is to regard the SOM as a model of natural language interpretation, and explicate its use in natural language processing (NLP) applications, especially in information retrieval and data mining of large text collections (see websom.hut.fi).
In the following, four particular views of the SOM are given: 1. The SOM is a model of specific aspects of biological neural nets, 2. The SOM constitutes a representative of a new paradigm in artificial intelligence and cognitive modeling, 3. The SOM is a tool for statistical analysis and visualization, 4. The SOM is a tool for the development of complex applications.
Some applications require efficient construction of large maps. Searching the best-matching unit is usually the computationally heaviest operation in the SOM. Using a tree-structured SOM, it is possible to use hierarchical search for the best match (Koikkalainen and Oja, 1990,Koikkalainen, 1994). In this method, the idea is to construct a hierarchy of SOMs, teaching the SOM on each level before proceeding the next layer. Another speedup method for making the winner search faster, based on the idea of Koikkalainen, is presented in (Kohonen et al., 1996b).
Most SOM applications use numerical data. The purpose of the present thesis is to demonstrate that statistical features of natural text can also be regarded as numerical features that facilitate the application of the SOM in NLP tasks.